轮胎系统是乘用车的重要组成部分。德国大陆汽车、Polytec和戴姆勒公司密切合作，共同分析了E-class车前轮轴上的轮胎系统的三维振动。利用有限元方法建立滚动轮胎的数学模型，并与车辆模型耦合。本次试验使用Polytec公司的三维扫描式激光多普勒测振仪对整车NVH性能进行测试，并验证模型的有效性。

高复杂性：一个轮胎含有20多个部件

轮胎系统的主要功能是为了支撑车重，并在加速、刹车和转弯时，将力传递到路面上。此外，它还负责减少因不规则路面所带来的振动和噪声，提高乘客的乘坐舒适性。随着内燃机的噪声降低、新的驱动系统的出现、及车辆零部件的轻量化，轮胎系统的第二功能变得越来越重要。

除了对轮胎的噪声、振动和声振粗糙度（NVH）性能的要求越来越高之外，降低开发成本和时间的需求也日益迫切，我们需要精确有效的数值方法来辅助开发过程。

由于若干因素，对轮胎系统的理解和数学建模极具有挑战性。首先，虽然轮胎的外胎、轮辋和内腔可以被认为是两种固体结构和一种封闭的流体，但仅外胎就含有20多个部件。每个部件由一个或多个非线性材料组成，其性能取决于温度、应变率、应变幅值和应变史。其次，轮胎的激励发生在与路面的接触处，因此是路面形状与外胎在接触面的非线性动态响应函数。

对于振幅较小以及频率在20 ~ 400Hz之间的，可以使用模态模型来有效地描述轮胎响应。基于轮胎阻尼的复杂分布、滚动产生的回转力以及轮胎内外胎-轮辋与空腔之间的耦合等因素，滚动轮胎系统一般采用最通用的模态模型。

本次试验中，在车辆单轮上加上受控运动激励。三维扫描式激光多普勒测振仪加上合理位置摆放的反射镜，可以测量旋转轮胎大部分可见表面。振幅的精确测量不仅可以帮助加深理解系统的动态特性，还可以验证复杂的数学模型和预测结果。

数学模型

根据结构质量矩阵M_s、结构刚度矩阵K_s、流体质量矩阵M_f、流体刚度矩阵K_f，从有限元模型来引出结构的物理特性。由于气腔与结构之间的耦合作用（使用H_sf矩阵来描述）,系统矩阵呈非对称性[1]。在对车轮进行非线性静力加载和滚动后使用任意拉格朗日-欧拉法（ALE），运动方程可表示为式(1)

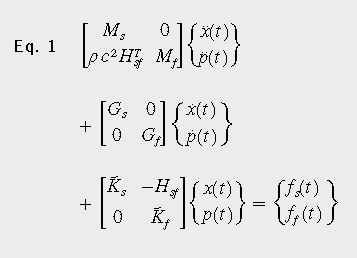
这里，ρ为空气密度，c是声速，G_s是结构的反对称陀螺矩阵，G_f是流体的反对称陀螺矩阵。时变量分别为位移x、声压p和力f。

为得到标准特征值形式[2]，需要根据式2（a）和2（b）将式1中的N×N二阶微分方程， 变换成2N×2N一阶微分方程。

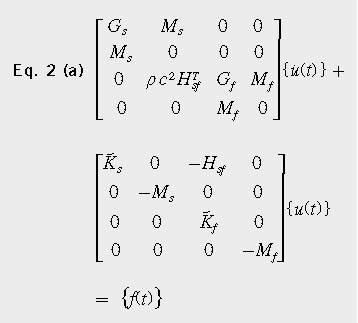
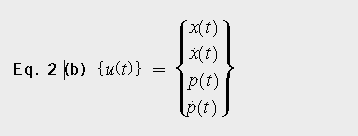
由于方程式2中的非对称性矩阵，本征解将包含单一特征值矩阵[s_r]和两组复杂的特征向量[Θ_LH]和[Θ_RH]。右边的特征向量（RH）描述模态振型，左边的特征向量（LH）描述激励振型。复模态不仅具有与实模态相同的振幅，而且还具有相位，以行波的形式出现；这与用驻波可更好地描述的实模态形成了对比。

轮毂的边界条件描述

车轮与车辆子结构的耦合可以通过空间模型、模态模型或响应模型来实现。本文采用后一种方法来计算车轮与车辆的耦合振动响应。耦合响应方法是建立在两个子结构共有界面的自由度的相容性和平衡条件的基础上。通过位移导纳方法，由[H_A]和[H_B]两个非耦合FRF矩阵计算出耦合FRF矩阵[H_C]，如方程式3所示：

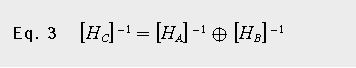
车轮子结构的位移导纳，即单位力下的位移量，由模态模型计算得出。这种响应方法的一个优点是，由于轮辋和轮毂之间的耦合点需要的自由度很少，因此变换后的矩阵非常简洁，如方程3所示。

图1 所测车辆有限元模型，底盘上约有200万个节点

图1 显示的是本次实验所用的车辆有限元模型，包括底盘细节（大约200万个节点）、动力总成和完整的车身结构（大约500万个节点）。

通过计算轮毂在六个方向上的位移导纳矩阵F/X，获得用于轮胎与车辆连接的36个频响函数（FRF）。通过轮毂中心到底盘或车身点可进一步计算出频率响应函数。

测试装置

如图2所示，大陆汽车公司的试验台使用了Polytec公司的3D扫描式激光多普勒测振仪[3,4]。右前轮胎置于转鼓上。

图2 左侧为3D扫描式激光测振仪，右侧为转鼓试验台

滚筒表面做了轻微不均匀性处理，并施加一个已知的激励并确保轮胎和转鼓始终保持接触。在有限的频率集下，对轮胎的每一速度施加一定频率范围的运动激励，频率与转鼓转速成正比。

车轮由转鼓驱动，速度恒定在33至99km/h之间（3km/h为速度增加步长）。在每个恒定速度上，从9个不同的角度扫描车轮，其中四个不同角度是来自于车轮后方的反射镜。

为获取三维振动工作响应向量，使用三个不同测量方向的扫描头进行振动测试。测振系统的光学头探测到轮胎表面沿着激光方向上的多普勒频移，这与其瞬时振动速度成正比。通过坐标变换，获取振动矢量的x、y和z分量。通过三束激光同步扫描，可以测量包括相位在内的振动特性。

测试结果

车轮的响应，或者说车内噪声，很大程度上是由轮胎的前几阶模态所决定。这些模态振型在轴上产生很大的合力，通常是一阶模态，即一阶左右平动模态、一阶上下平动模态、一阶空腔谐振模态等。

在测量滚轮的过程中，记录了驾驶舱内四个位置的声压级。在300Hz以下，可以很容易地识别这些信号的频谱峰值，以及相应频率下车轮的工作变形（ODS），如图3所示。可以预料的是，很多这样的点都是由ODS变形导致的。

图3 90 km/h时的胎面变形

滚动轮胎系统的ODS可以在测得频率计算得出。为此，首先使用响应耦合法计算出轮轴之间界面自由度上的力。然后将这些力与接触处的运动激励一起应用于模态轮胎模型。这样，可将车轮表面振动特性的计算值和测量值进行比对。

表1显示的是同位移比例下，计算和测量出的几个重要的轮胎响应的ODS结果的对比。不同颜色代表不同的瞬时速度。令人高兴的是，我们可以看到在速度最高99km/h的范围内，计算出来的ODS都可以通过测试得到相同的结果。旋转的关键之处[5,6]在试验和计算中都在控制之内。

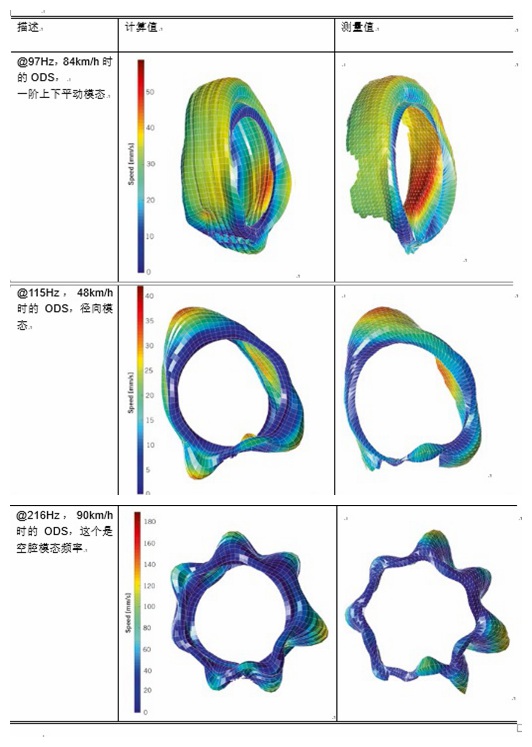
表1 几个频率下计算和测量的ODS对比

总结和展望

本文采用创新的非接触式激光测振技术结合先进的轮胎和车辆模型，对轮胎滚动噪声和振动进行了详尽的研究。试验结果表明，尽管这两个领域的科研均具有挑战性，但计算结果和测量结果具有很好的一致性。

本研究使用的轮胎模型仅根据设计参数而建立，并没有使用轮胎物理数据。在研发过程，轮胎在正式投入生产前需要数字预测，而激光测振仪可以提供大量高质量测试数据对模拟数据进行验证，促进模型的进一步升级。同时，测得结果还能帮助用户更好地理解滚动轮胎的机械性能，在大量轮胎样品测试的基础上，使用与本文相同的测试方法，可验证仿真的质量，这是开发早期阶段的数字方法的基础，可提升车轮与车辆的NVH性能。

鸣谢

本项目得到Ingo Busch、戴姆勒公司车身&底盘NVH测试部门、以及德国大陆汽车公司轮胎力学和NVH工程部门的Achillefs Tsotras博士和Diogo Baptista博士等的大力支持，感谢所有相关方的合作和支持。